Recently financial applications attracted a renewed interest from the Artificial Intelligence (AI) community since the global crises demonstrated the importance of sound financial modeling and reliable data processing. Financial markets produce vast amounts of temporal data ranging from stock prices to interest rates making them ideal mediums to apply machine learning methods. Furthermore, due to the integration of high performance, low-latency computing resources and financial data collection infrastructures, a wide range of machine learning algorithms could be readily leveraged with full potential in financial stock markets.
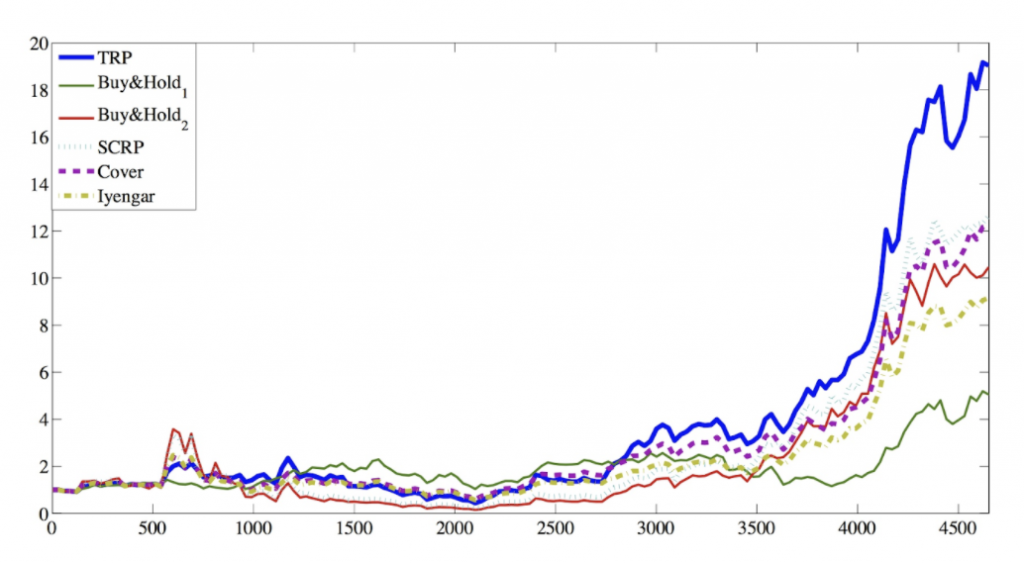
In particular, our research focuses on the portfolio selection problem, which is one the most important financial applications and has already attracted substantial interest from the AI community. In particular, we study investment in a financial market having a finite number of assets. We concentrate on how an investor should distribute capital over these assets and when he/she should reallocate the distribution of the funds over those assets in time to maximize the overall cumulative wealth. In financial terms, distributing one’s capital over various assets is known as the portfolio management problem and reallocation of this distribution by buying and selling stocks is referred to as the rebalancing of the given portfolio. Due to obvious reasons, the portfolio management problem has been investigated in various different fields from financial engineering, signal processing to information theory, with a significant room for improvement as the recent financial crises demonstrated. To this end, we investigate the portfolio management problem in discrete-time markets when the market levies proportional transaction costs in trading while buying and selling stocks, which accurately models a wide range of real life markets.
Sample publications:
S. S. Kozat, A. C. Singer, “Universal semiconstant portfolios,” Mathematical Finance, vol. 21, no. 2, pp. 293-311, April 2011.