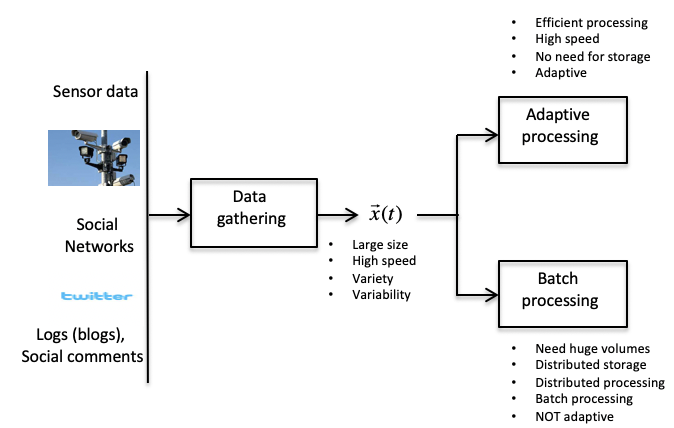
Due to the rapid developments in sensor technologies, wide spread usage of smart phones and Internet, we have the opportunity and capability to gather huge amounts of data in different real life Artificial Intelligence (AI) applications (which was not possible in the past). Efficient and effective processing of this big data can significantly improve the performance of many machine learning algorithms. However, this big data has dimensions and volumes unseen before in AI problems, comes in different varieties and its quality, quantity and statistics rapidly change in time and among elements. To accommodate these problems, the big data should be processed online algorithms by machine learning methods since the online methods (1) can process the data in sequential manner, i.e., instantly, without any storage requirement, (2) can constantly adapt to the changing statistics or quality of the data, hence can be robust and prone to variations and uncertainties.
However, since the classical adaptive machine learning approaches are designed for inputs that have much smaller dimensions and fewer variations, these methods cannot be used effectively or efficiently to process the big data (or cannot even operate due to computational issues). Hence, in order to effectively process the big data, we (1) develop novel online learning algorithms specifically tuned to effectively operate on large dimensional data, (2) demonstrate the effectiveness and efficiency of these approaches in different applications and prove these results mathematically, and finally (3) construct the big data based machine learning framework, as the first time, by defining new cost measures and design methodologies. This is the first research effort that is aimed to introduce a new framework for online processing of big data and to construct novel machine learning algorithms that are shown to be effective, efficient and robust on big data.
Sample publications:
N. D. Vanli and S. S. Kozat, “A Unified Approach to Universal Prediction: Generalized Upper and Lower Bounds,” IEEE Transactions on Neural Networks and Learning Systems, 2013.
N. D. Vanli, M. O. Sayin and S. S. Kozat, “Twice Universal Piecewise Linear Regression via Infinite Depth Context Tree Weighting Method,” IEEE Transactions on Neural Networks and Learning Systems, 2013.
H. Ozkan and S. S. Kozat, “Data Imputation through the Identification of Local Anomalies,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013.